Tutorial 2. Estimating the volume of a body

<< Tutorial 1. Getting started

Back to the list of tutorials

Tutorial 3. Estimating the multivariate integral >>

In this tutorial we are going to demonstrate one of the possible applications of \((t, m, s)\)-nets, namely, the approximate calculation of body volume. For our educational purposes we are going to consider a three-dimensional octahedron \(\Sigma\) with vertices \((0.5,0.5,0)\), \((0,0,0.5)\), \((1,0,0.5)\), \((1,1,0.5)\), \((0,1,0.5)\), \((0.5,0.5,1)\). You may see \(\Sigma\) inscribed into a three-dimensional unit cube in a figure below.

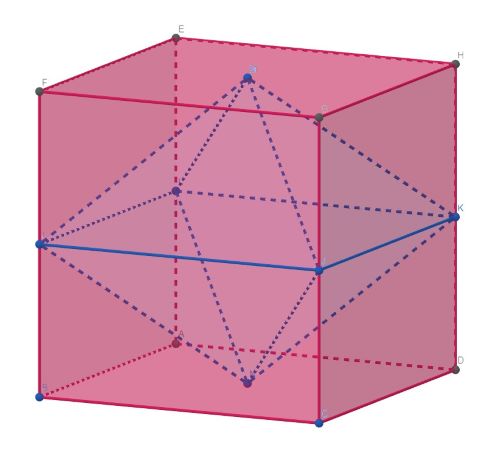
To estimate the volume of \(\Sigma\) signified hereafter with \(V(\Sigma)\) we may saturate the unit cube with some \((t, m, s)\)-net and use the following formula:

\[V(\Sigma) \approx \frac{|N \cap \Sigma|}{|N|}\]

where \(N\) is the constructed \((t, m, s)\)-net. Speaking in plain English, the approximate value of volume can be found as a ratio of the number of net points that ended up inside of the octahedron to the total number of net points.

1. Basic workflow

Let us assume the same file structure as in the previous tutorial. Thus, we need to open and edit an empty main.cpp file that will contain the code for our desired program.

It is quite natural to state that in order to get an accurate estimation of \(V(\Sigma)\) we need to generate a rather huge net. Let us start, then, with construction of a three-dimensional net with, say, \(2^{20} = 1,048,576\) points.

#include "libraries/tms-nets/tms-nets.hpp"
#include <cstdint> // needed for uint*_t types
 
int main()
{
    uint32_t const                      tms_net_point_count = 1UL << 20;
    tms::Niederreiter                   tms_net(20, 3);
 
    return 0;
}

After that we just need a loop that will traverse all points of our net and count how many of them are inside of \(\Sigma\).

#include "libraries/tms-nets/tms-nets.hpp"
#include <cstdint> // needed for uint*_t types
#include <iostream> // needed for output
 
int main()
{
    uint32_t const                      tms_net_point_count = 1UL << 20;
    tms::Niederreiter                   tms_net(20, 3);
 
    uint32_t                            inside_point_count = 0;
 
    for (uint32_t point_i = 0; point_i < tms_net_point_count; ++point_i)
    {
        tms::Point current_point = tms_net.generate_point(point_i);
        inside_point_count += isPointInside(current_point);
    }
 
    // We transform inside_point_count into a floating-point type defined in our library
    std::cout << "V(Sigma) = " << ((tms::Real)(inside_point_count) / tms_net_point_count) << '\n';
 
    return 0;
}

2. Identify points within the octahedron

The only thing missing in our program is the aforementioned function isPointInside that would return true, if the given point is inside of the octahedron, and false, otherwise.

As we may notice, \(\Sigma\) is symmetric about the plane \(z = 0.5\). Knowing this, we may state that there exists a function \(\Delta(x,y)\) such that for any three-dimensional point \(a = (x, y, z)\) it is true that \(a \in \Sigma \Leftrightarrow 0.5 - \Delta(x,y) \le z \le 0.5 + \Delta(x,y)\). \(\Delta(x,y)\) can be expressed in the following way: \(\Delta(x,y) = 0.5 - \max \{|x - 0.5|, |y - 0.5|\}\). Let us now code this in C++.

#include "libraries/tms-nets/tms-nets.hpp"
#include <cstdint> // needed for uint*_t types
#include <iostream> // needed for output
#include <algorithm> // needed for max
#include <cmath> // needed for fabs
 
bool isPointInside(tms::Point &point)
{
    // To calculate the value of Delta, we are going to use a floating-point type defined within our library
    tms::Real Delta = 0.5 - std::max(std::fabs(point[0] - 0.5), std::fabs(point[1] - 0.5));
 
    return (point[2] >= 0.5 - Delta) && (point[2] <= 0.5 + Delta);
}
 
int main()
{
    uint32_t const                      tms_net_point_count = 1UL << 20;
    tms::Niederreiter                   tms_net(20, 3);
 
    uint32_t                            inside_point_count = 0;
 
    for (uint32_t point_i = 0; point_i < tms_net_point_count; ++point_i)
    {
        tms::Point current_point = tms_net.generate_point(point_i);
        inside_point_count += isPointInside(current_point);
    }
 
    // We transform inside_point_count into a floating-point type defined in our library
    std::cout << "V(Sigma) = " << ((tms::Real)(inside_point_count) / tms_net_point_count) << '\n';
 
    return 0;
}

The expected output is:

V(Sigma) = 0.333347

To check our answer let us find the precise value of \(V(\Sigma)\) with the help of the formula: \(V(\Sigma) = \frac{1}{3}Sh\) where \(S\) is the square of the base and \(h\) is the distance between two opposing vertices about the base. If we substitue, we get \(V(\Sigma) = \frac{1}{3} \cdot 1 \cdot 1 = \frac{1}{3}\). As we see, our estimation is pretty accurate.

<< Tutorial 1. Getting started

Back to the list of tutorials

Tutorial 3. Estimating the multivariate integral >>