Tutorial 1. Getting started

Back to the list of tutorials

Tutorial 2. Estimating the volume of a body >>

In this tutorial you will get acquainted with the most basic functionality of the library. The goal of this exercise is to generate a ready-to-use \((t, m, s)\)-net.

1. Preparations

We assume that before reading this tutorial you already downloaded the library and unpacked its files. If you didn't, visit the Download page. We also assume your decent knowledge of C++.

Note

These tutorials only cover the features of the latest stable version of the library.

Let us now create a sample project for the purposes of this tutorial. You may do this however you prefer: manually or with the help of your most favourive IDE. Hereafter we assume that our sample project has the following file structure.

sample_project_root_folder
 ├─ libraries
 │   ├─ tms-nets
 │   │   └─ ... there go the files of our library ...
 │   ├─ tms-nets.a
 │   └─ tms-nets.hpp
 └─ main.cpp

File main.cpp was created manually and it is currently empty.

Note

Do not forget to enable C++17 standard in your compiler!

2. Create a new net

Let us now open and edit main.cpp file of our sample program. There, in order to use our library, we first need to include the file with needed functionality. Say, we want to generate a \((t, m, s)\)-net using Niederreiter's algorithm. Hence, we need to include the following file:

#include "libraries/tms-nets/tms-nets.hpp"

The functionality of our library is completely stored within a sole namespace called tms. In particular, the Niederreiter's \((t, m, s)\)-nets in base \(2\) will be represented as the objects of class tms::Niederreiter. Each digital net has the parameters \(t\), \(m\) and \(s\) as its invariants meaning that if at some moment of time you need to change their values, you'll have to create a new net. These parameters have the following meaning:

• \(t\) : this non-negative integer parameter signifies the "quality of points' dispersion" within the unit cube. More precisely, the less its quantity is, the lower is the discrepancy of the net. Minimal possible value of \(t\) increases with the growth of dimension;
• \(m\) : this non-negative integer parameter signifies the binary logarithm of number \(M\) of points within the net, i.e., \(m = \log_2 M\). Please remember that \(M\) must always be a power of \(2\). Minimal possible value of \(m\) is \(t\) and, hence, it increases with the growth of dimension as well;
• \(s\) : positive integer dimension of the unit cube that we wish to fill with net's points.

If you want to find out mathematically rigorous description of parameter \(t\), check out the sources from Recommended literature. However, if you don't want to go deep into the theory, you shall not despair, since our generator is capable of automatic selection of the best (i.e., the lowest) possible \(t\) for each particular case. Having this, you may just forget about its existence (as long as your value of \(m\) is sufficiently large to satisfy \(m \ge t\); don't worry: if your value of \(m\) is too small for a particular \(s\), our library will inform you about that with the help of a runtime exception).

Let us now write a program that saturates a two-dimesional unit cube (i.e., a square with the length of each edge being equal to \(1\)) with a \((t, m, s)\)-net containing \(16\) quasirandom points. Here, \(s = 2\) (since the unit cube is two-dimensional) and \(m = \log_2 M = \log_2 16 = \log_2 2^4 = 4\). Knowing this, we may finally create a new net with the help of the following constructor.

tms::Niederreiter(tms::BasicInt const nbits, tms::BasicInt const dim)

Here nbits shall be replaced with \(m\) and dim shall be replaced with \(s\). Having this said, we may write the following piece of code.

#include "libraries/tms-nets/tms-nets.hpp"
 
int main()
{
    tms::Niederreiter my_first_net(4, 2);
 
    return 0;
}

Thus, my_first_net is the \((t, 4, 2)\)-net (value of \(t\) is still unknown) which was constructed with Niederreiter's algorithm and consists of \(16\) distinct quasirandom points within two-dimensional unit cube.

3. Check the parameters of the net

Let us now quickly verify the parameters \(t\), \(m\) and \(s\) of our net. Since \(m\) and \(s\) are defined by user, their values can be retrieved from the net by the calls of respective member functions m and s. As for the parameter \(t\), its value requires some additional analytical calculations which is why it can be retrieved with the special function t contained within tms::analysis namespace:

tms::BasicInt tms::analysis::t(DigitalNet const &net)

Here, net should be replaced with our digital net. The complete code may look as follows:

#include "libraries/tms-nets/tms-nets.hpp"
#include <iostream> // to perform output
 
int main()
{
    tms::Niederreiter my_first_net(4, 2);
 
    std::cout << "Parameters of my_first_net:\n";
    std::cout << "\tt = " << tms::analysis::t(my_first_net) << '\n';
    std::cout << "\tm = " << my_first_net.m() << '\n';
    std::cout << "\ts = " << my_first_net.s() << '\n';
 
    return 0;
}

The expected output is:

Parameters of my_first_net:
    t = 0
    m = 4
    s = 2

As we see, we were able to reach the value \(t = 0\) which is the lowest possible ever. You may spend a couple of minutes of your pastime on checking how the automatically chosen value of \(t\) changes with the growth of \(s\).

4. See the points of the net

Let us finally see the points! In order to optimise the consumption of resources our my_first_net doesn't actually store all its points in the memory. Instead, it calculates their coordinates on the fly right at the moment when we request them. To do this we are going to use the

tms::Point tms::Niederreiter::generate_point(tms::CountInt const pos)

method. Its only argument pos specifies the ordinal index of the point we wish to get. Since we want to take a look at not a single point of our new but all \(16\) points at once, we should wrap the call of this method in a loop.

#include "libraries/tms-nets/tms-nets.hpp"
#include <iostream>
 
int main()
{
    tms::Niederreiter my_first_net(4, 2);
 
    std::cout << "Parameters of my_first_net:\n";
    std::cout << "\tt = " << tms::analysis::t(my_first_net) << '\n';
    std::cout << "\tm = " << my_first_net.m() << '\n';
    std::cout << "\ts = " << my_first_net.s() << '\n';
 
    for (unsigned int point_i = 0; point_i < 16; ++point_i)
    {
        my_first_net.generate_point(point_i);
    }
 
    return 0;
}

If you compile this code, you will see that it is still quite useless. Let us add the output of our points to finally see their coordinates!

#include "libraries/tms-nets/tms-nets.hpp"
#include <iostream>
 
int main()
{
    tms::Niederreiter my_first_net(4, 2);
    
    std::cout << "Parameters of my_first_net:\n";
    std::cout << "\tt = " << tms::analysis::t(my_first_net) << '\n';
    std::cout << "\tm = " << my_first_net.m() << '\n';
    std::cout << "\ts = " << my_first_net.s() << '\n';
 
    std::cout << "\nGenerated points:\n";
    for (unsigned int point_i = 0; point_i < 16; ++point_i)
    {
        tms::Point current_point = my_first_net.generate_point(point_i);
        for (unsigned int dim_i = 0; dim_i < 2; ++dim_i)
        {
            std::cout << current_point[dim_i] << '\t';
        }
        std::cout << '\n';
    }
 
    return 0;
}

The expected output is:

Parameters of my_first_net:
    t = 0
    m = 4
    s = 2
 
Generated points:
0   0
0.5 0.5
0.75    0.25
0.25    0.75
0.375   0.375
0.875   0.875
0.625   0.125
0.125   0.625
0.1875  0.3125
0.6875  0.8125
0.9375  0.0625
0.4375  0.5625
0.3125  0.1875
0.8125  0.6875
0.5625  0.4375
0.0625  0.9375

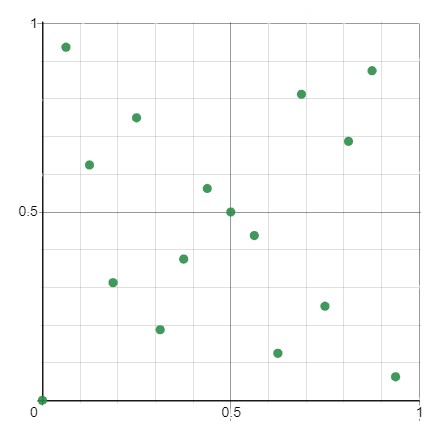
Let us visualise our net with the help of a thirdparty plotter (feature is not included into the library).

Back to the list of tutorials

Tutorial 2. Estimating the volume of a body >>