Metric graphs

The concept of metric graph extends the classical understanding of graphs in the following manner. Metric graph is defined as a graph \((V,E)\) where \(V\) is a set of vertices, \(E \subset V^2\) is a set of edges with each edge \(e \in E\) being associated with a certain interval \([0,l(e)]\), where \(l(e) > 0\) is called a length of the edge. Edge \((v,w) \in E\) is called directed ('from \(v\) to \(w\)'), if \((w,v) \notin E\). Otherwise, if \((w,v) \in E\), the edge \((v,w) \in E\) is called undirected ('from \(v\) to \(w\)', or 'between \(v\) and \(w\)').

This implementation also binds general theory by following additional restrictions:

• \(V \subset \{0,1,2,...,2^{32}-1\}\) (i.e., vertices can only be represented as non-negative integers up to \(2^{32}-1\));
• \(\{(v,w),(w,v)\} \subset E \Rightarrow l((v,w)) = l((w,v))\) (i.e., if one can go both ways, the distance between end points is the same).

For undirected edges, any point \(a \in [0,l((v,w))]\) will be considered the same with the point \(l((w,v)) - a \in [0,l((w,v))]\).

Thus, the main difference between metric graphs and non-metric graphs can be briefly stated by possibility of interpreting edges of a metric graph as geometric objects where distance can be measured not only between vertices of the graph itself, but also between points on intervals \([0,l(e)]\) that correspond to the edges. Collectively, they will be noted as points of the graph.

You may read more about metric graphs here.

Random walk

Random walk of an agent \(A(t)\) on a metric graph \(G\) is a continuous-time random process that is described as follows:

1. \(t \in T = \{\tau \in \mathbb{R} | \tau \ge 0\}\) (time is non-negative);
2. \(A(t)\) maps a moment of time to some point of the graph;
3. \(A(t)\) is continuous;
4. if \(A(t) = v \in V\), the point \(A(t + \delta t)\) is chosen randomly among all points of all edges outgoing from \(v\);
5. if \(A(t) = p \notin V\), \(A(t + \delta t) - A(t) = A(t) - A(t - \delta t)\) (direction of a walk cannot be changed while on edge, the speed of a point is constant);
6. if \(A(t) = v \in V\) and \(A(t + \delta t) = p \notin V, p \in [0, l((v,w))]\) where \((v,w) \in E\), then \(\min \{\tau \in T | \tau > t, A(\tau) = w\} = t + l(e)\) (the time that it takes to walk from vertex \(v\) to vertex \(w\) equals the length of the corresponding edge).

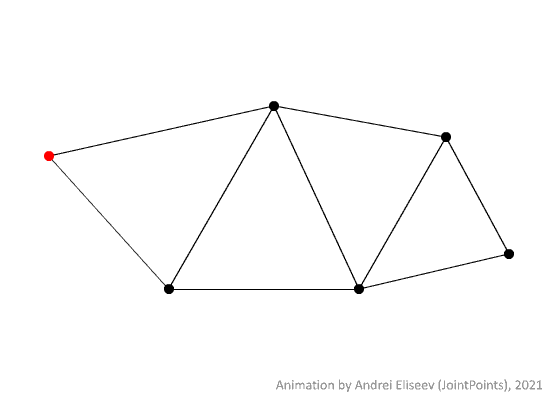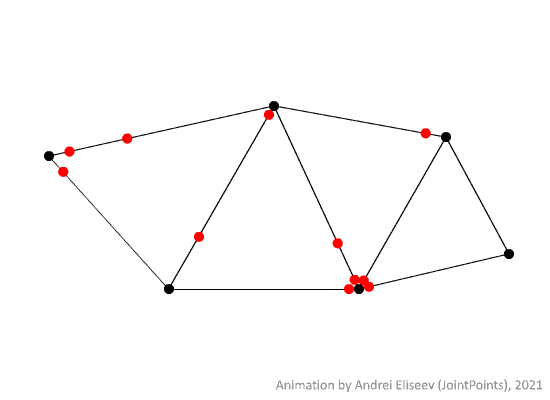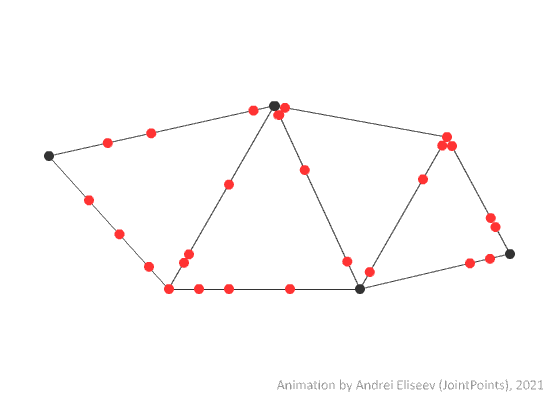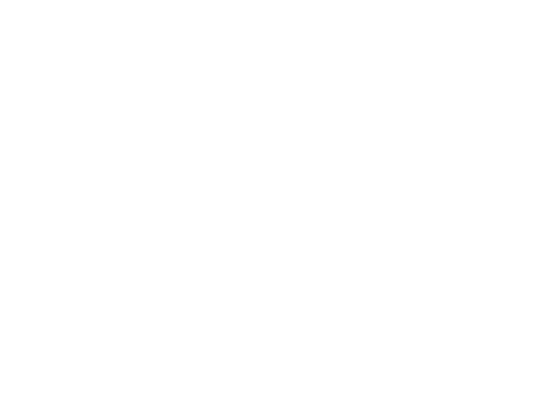
An example of a random walk of a point on a metric graph can be seen below.

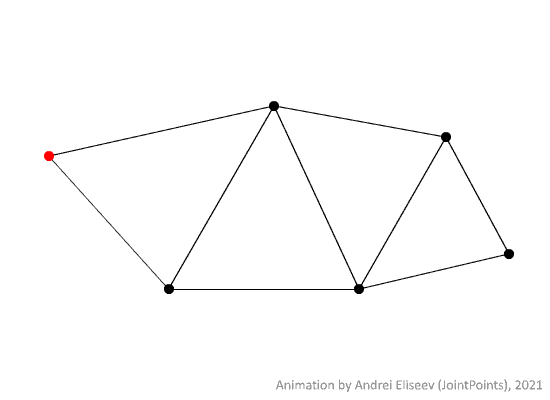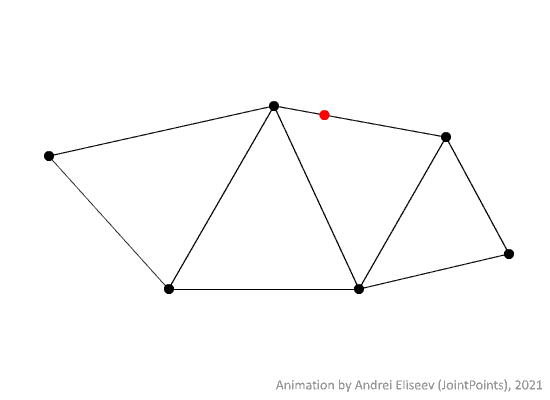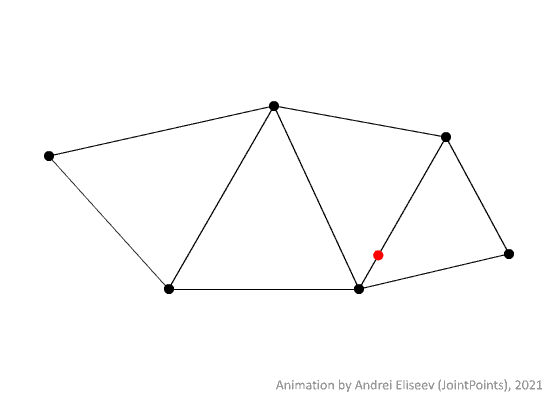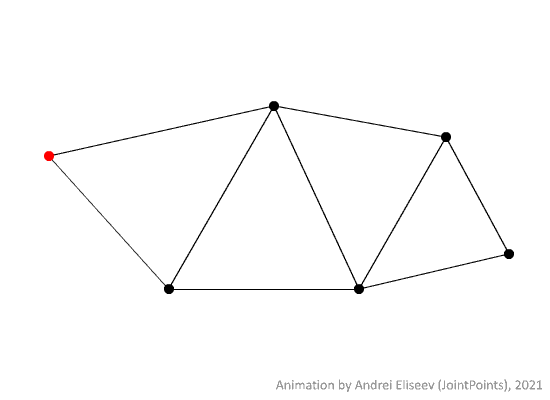
However, it is usually inconvenient to consider a single instance of a random walk since it gives little to no information about the general behaviour of the process. That is why a collection of all possible random walks with the same initial conditions is preferrable to study instead. Such a collection can be seen below.

This kind of a structure will be called an RW-space over a metric graph. Please, note that "RW-space" is a non-standard term, i.e. it may not be used widely among other people who study random walks.